mathematica软件的常用操作3——复数操作、矩阵运算、其他操作|热议
复数操作:主要运算有求模、求幅角、求实部、求虚部、求共轭。
 (资料图片仅供参考)
(资料图片仅供参考)
不含未知数的复数:
求复数的模:
Norm[1/(2 + 2 I)],其中I(大写的i)表示虚数单位,输出为:1/(2 Sqrt[2])。
也可以用Abs[1/(2 + 2 I)],输出结果一样的。
求复数的幅角:
Arg[1/(2 + 2 I)],输出为:-pi/4。
求共轭复数:
Conjugate[1/(2 + 2 I)],输出为:1/4 + I/4。
求实部:
Re[1/(2 + 2 I)],输出为:1/4。
求虚部:
Im[1/(2 + 2 I)],输出为:-(1/4)。
含未知数的复数:
求实部:
输出为:(2 - w^2)/(4 - 3 w^2 + w^4)
求虚部:
输出为:-(w/(4 - 3 w^2 + w^4))
求复数的模:
输出为:1/Sqrt[4 - 3 w^2 + w^4]。其中Sqrt表示根号。
求复数的幅角:
其中第二行为对应的输出结果。代入一个数值,如w=2,可得如下结果:
求共轭复数:
复数展开:
也可以用如下方式进行复数展开:
其中第二行为输出,可以清晰的看到实部和虚部。
矩阵操作:
定义矩阵:
里面以后有三个大括号,表示三行,每个大括号里面有三个数据,表示三列,所以这是一个三行三列的矩阵,这个矩阵就是电力电子里面的坐标变换矩阵。
矩阵的乘积:
上图第二块为输出结果,a为3行3列,后面乘了一个列矩阵,最终结果为3行1列,就是线性代数中的矩阵运算。通过这种软件求解含有未知数的矩阵运算很方便。
求逆矩阵:
转置矩阵:
其他操作:
弧度角度转换:
*180 /Pi // Degree,弧度转角度操作,输出结果为:
转小数:
Sqrt[3] // N,输出结果为:。
可以按键盘esc sqrt tab ,这是生成根号符号的快捷方式。
mathematica这款软件的基本操作到这里就给大家介绍完毕了,希望大家都能有所收获,学会使用这强大的利器。工欲善其事必先利其器!!!
有所收获的同时可以动动小手点赞支持一下哟。
关键词:
精心推荐
- mathematica软件的常用操作3——复数操作、矩阵运算、其他操作|热议
- 全球热点!海河水利委员会组织开展海河防潮闸除险加固工程跟踪审计工作
- 上巳节又被称为什么节 上巳节
- 广东:引导药品储运配送资源适当向偏远地区倾斜|全球热消息
- 电池安全还不够,吉利银河L7告诉你“为什么3挡比单挡强” 世界速讯
- 你会删除不常联系的同学吗?女生毕业删除90%同学被骂有病:留着也没用_当前独家
- 2023年全球城市排名出炉:上海比北京国际化更强?|最新
- 阿里纳斯:现在大洛、霍福德、西卡在打中锋 文班的对抗不是问题 世界今热点
- 10000mAh车规级电芯 魅族PANDAER×SHARGE移动电源图赏
- 郑州市2023荷花展28日开幕 紫荆山公园7000株荷花绽放
- 青海囊谦:红外相机多次记录到国家一级保护动物金钱豹
- 3899元!OPPO Reno10 Pro星籁版今日开启预售-当前速讯
- 世界观速讯丨阿斯顿·马丁:未来5年内将投资近20亿英镑推动电动化转型
- 虚拟人的硬件和软件调试篇(其一)
X 关闭
X 关闭
产业
-
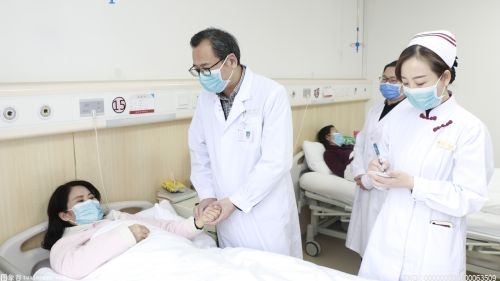
不用跑北京 在家门口也能挂上顶...
日前,我省首个神经疾病会诊中心——首都医科大学宣武医院河北医院...
-

“十四五”期间 河北省将优化快...
从省邮政管理局获悉,十四五期间,我省将优化快递空间布局,着力构...
-

张家口市宣化区:光伏发电站赋能...
3月19日拍摄的张家口市宣化区春光乡曹庄子村光伏发电站。张家口市宣...
-
“张同学”商标被多方抢注 涉及...
“张同学”商标被多方抢注,官方曾点名批评恶意抢注“丁真” ...
-

山东济南“防诈奶奶团”花式反诈...
中新网济南12月15日电 (李明芮)“老有所为 无私奉献 志愿服...
-

广州新增1例境外输入关联无症状...
广州卫健委今日通报,2021年12月15日,在对入境转运专班工作人...
-

西安报告初筛阳性病例转为确诊病例
12月15日10:20,经陕西西安市级专家组会诊,西安市报告新冠病毒...
-
广东东莞新增本土确诊病例2例 ...
(抗击新冠肺炎)广东东莞新增本土确诊病例2例 全市全员核酸检测...
-

中缅边境临沧:民警深夜出击捣毁...
中新网临沧12月15日电 (胡波 邱珺珲)记者15日从云南临沧边境...
-

“土家鼓王”彭承金:致力传承土...
中新网恩施12月15日电 题:“土家鼓王”彭承金:致力传承土家...






