当前热讯:样本方差服从什么分布(为什么样本方差服从卡方分布?请帮忙证明一下)
本文目录一览:
 (资料图片仅供参考)
(资料图片仅供参考)
为什么样本均值分布服从自由度n的卡方分布,而样本方差分布服从自由度n-1的分布?
样本均值分布服从自由度n的卡方分布,而样本方差分布服从自由度n-1的分布是因为:通过一个引理,就是标准正态变量的随机分布服从自由度为1的卡方碧中颂分布,以及服从卡方分布的随机变量和仍服从卡方悔郑分布且自由度为原随机变量自由度之和。然后在通过归纳法证明。
样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是会有偏差,是会低估了总体的样本方差的。为了能无偏差的估计总体方差,所以要对方差计算公式进行修正,修正后就得到(n-1)*样本方差与总体方差之比服从自由度为n-1的卡方分布。
常常把一个式子中
独立变量的个数称为这个式子的“自由度”,确定一个式子自由度的方法是:若式子包含有 n 个变量,其中k 个被限制的样本统计量,则这个表达式的自由度为 n-k。比如中包含ξ1,ξ2,…,ξn这 n 个变量,其中ξ1-ξn-1相互独立培御,ξn为其余变量的平均值,因此自由度为 n-1。
为什么样本方差服从卡方分布?请帮忙证明一下
不是样本方差服从卡方分布。应该是(n-1)S2/σ2服从(n-1)卡方分布,这个证明需要用到矩阵知识,记住有这个就可以。
卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。穗山
扩展资料:
在抽样分布理论一节里讲到,从正态总体进行一次抽样就相当于独立同分布的 n 个正态随机变量ξ1,ξ2,…,ξn的一次取值,将 n 个随机变量针对总体均值与方差进行标准化得(i=1,…,n),显然每个都是服从标准正态分布的。
若式子包含有 n 个变量,其中k 个被限制的样本统计量,则这个表达式的自由度为 n-k。比如中包含ξ1,ξ2,…,ξn这 n 个变量,笑族稿其中ξ1-ξn-1相互独立,ξn为其余变量的平均值,碰孝因此自由度为 n-1。
以上就是小编对样本方差服从什么分布的相关信息分享,希望能对大家有所帮助。
关键词:
精心推荐
- 当前热讯:样本方差服从什么分布(为什么样本方差服从卡方分布?请帮忙证明一下)
- 教育部部长:持续加强人工智能相关学科专业和平台载体建设 培养一大批人工智能高端人才
- 新西兰银行:财政预算增加了新西兰联储的压力,利率将升至5.75%;|当前独家
- 东北证券:中长期坚定看好AI+数据要素最强主线 推荐数据拥有方+数据能力提供方_世界热文
- 哈利波特3 阿兹卡班的逃犯_哈利波特3阿兹卡班的逃犯迅雷下载
- 全球今亮点!【聚焦世界智能大会】开幕啦!记者体验世界智能大会“黑科技”
- 环球微资讯!北京21项举措抢抓人工智能大模型机遇
- 梅西如愿封王,恩师能否圆梦?曼城约战国米,瓜帅欲一战粉碎质疑
- 环球播报:湖南农大与浏阳市合作共建浏阳校区 明年3月投入使用
- 库尔图瓦赛后道歉!皇马欧冠惨败,巴萨欢庆,哈维祝贺瓜迪奥拉 世界新消息
- 徐翔带领散户先胜一筹!泽熙、华丽家族(600503.SH)争端“白热化” 8年股价暴跌九成引不满
- 瘤内基因编辑增效ACT疗法研究获进展-天天快资讯
- 我武生物05月17日被深股通减持12.26万股|今日热议
- 烟火里的尘埃表达的是什么_烟火里的尘埃表达什么 天天热点评
X 关闭
X 关闭
产业
-
不用跑北京 在家门口也能挂上顶...
日前,我省首个神经疾病会诊中心——首都医科大学宣武医院河北医院...
-

“十四五”期间 河北省将优化快...
从省邮政管理局获悉,十四五期间,我省将优化快递空间布局,着力构...
-

张家口市宣化区:光伏发电站赋能...
3月19日拍摄的张家口市宣化区春光乡曹庄子村光伏发电站。张家口市宣...
-
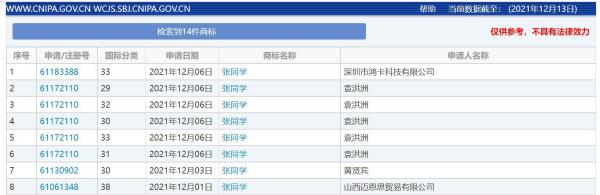
“张同学”商标被多方抢注 涉及...
“张同学”商标被多方抢注,官方曾点名批评恶意抢注“丁真” ...
-

山东济南“防诈奶奶团”花式反诈...
中新网济南12月15日电 (李明芮)“老有所为 无私奉献 志愿服...
-

广州新增1例境外输入关联无症状...
广州卫健委今日通报,2021年12月15日,在对入境转运专班工作人...
-

西安报告初筛阳性病例转为确诊病例
12月15日10:20,经陕西西安市级专家组会诊,西安市报告新冠病毒...
-
广东东莞新增本土确诊病例2例 ...
(抗击新冠肺炎)广东东莞新增本土确诊病例2例 全市全员核酸检测...
-

中缅边境临沧:民警深夜出击捣毁...
中新网临沧12月15日电 (胡波 邱珺珲)记者15日从云南临沧边境...
-

“土家鼓王”彭承金:致力传承土...
中新网恩施12月15日电 题:“土家鼓王”彭承金:致力传承土家...






